 time in a single individual after a single dose of 320
mg.
time in a single individual after a single dose of 320
mg.Chapter 2 - NONMEM Examples
In this chapter, two examples of the use of NONMEM will be given. The first estimates pharmacokinetic parameters of an individual from his data; the second estimates so-called population parameters from data from a group of individuals. The examples serve to introduce NONMEM notation, input and output, and to provide an idea of what is possible using the system. The second example will be discussed again in Chapter 11.
Figure 2.1 shows the
input used to fit a model to observations of theophylline
plasma concentration
 time in a single individual after a single dose of 320
mg.
time in a single individual after a single dose of 320
mg.
$PROB SIMPLE NONLINEAR REGRESSION - THEOPHYLINE $INPUT ID AMT TIME DV $DATA P2DATA $SUBROUTINE ADVAN2 $PK KA=THETA(1) K=THETA(2) V=THETA(3) S2=V $ERROR Y=F+ERR(1) $THETA (0, 1.7) (0, .102) (0, 29.) $OMEGA 1.2 $ESTIMATION PRINT=5 $COVARIANCE $TABLE ID AMT TIME $SCATTER PRED VS DV UNIT
Figure 2.1. The input (i.e., NM-TRAN control records) for analysis of some individual theophylline data.
The first line (record)
gives a name to the problem. The rest of the lines (records)
discuss the data, the model, and the desired output. Before
going into these in some greater detail, you may want to
look right now at figures 2.1 and 2.2, and then 2.4 and 2.5.
Figure 2.2 shows the data for this problem, and figures 2.4
and 2.5 show some of NONMEM’s output. All you need to
know to get a good idea of what this analysis shows is that
the one-compartment model with first-order absorption has
been used; the observed concentrations and the times of
observation after the bolus dose are in columns 4 and 3,
respectively, of figure 2.2; and that the symbol DV stands
for dependent variable (the observed concentrations, in this
case). You should, for example, even at this point, be able
to tell that the estimate of Volume of Distribution (V in
figure 2.1, and THETA(3) in figure 2.4) is 32 liters (L),
with a standard error of
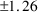 L. Now consider the figures in greater detail.
L. Now consider the figures in greater detail.
The second record of figure 2.1 names the data items that appear on each data record, and the third record gives the name of the file containing the data records, P2DATA in this example. Figure 2.2 shows the contents of P2DATA.
2 320. 0. 0.
2 0. .27 1.71
2 0. .52 7.91
2 0. 1. 8.31
2 0. 1.92 8.33
2 0. 3.5 6.85
2 0. 5.02 6.08
2 0. 7.03 5.4
2 0. 9. 4.55
2 0. 12. 3.01
2 0. 24.3 .90
Figure 2.2. The contents of the data file containing the data records.
According to the second record of figure 2.1, the third data item (column) of a data record is TIME, the time associated with the event described by that data record. The event at a given time (for this simple data set) can either be the administration of a dose or the acquisition of an observation. The second data item of a data record is AMT, amount (in this case in mg) of the dose given at TIME, the time of the record. Apparently, 320 mg is given at time zero (first record of figure 2.2), and no further doses are given (all zeros in column 2 thereafter). The fourth data item (column) in P2DATA is named DV, for Dependent Variable (the measured plasma theophylline concentration), as already mentioned. So, all of the data records, except the first, give the time after the 320 mg dose, and the concentration of theophylline (in mg/L) measured in a plasma sample drawn at that time. The first data item is labelled ID for the IDentification number of the patient. Here it happens to be 2.
The fourth record of figure 2.1 identifies the pharmacokinetic model PREDPP is to use: the one-compartment model with first-order absorption. It is implemented by an ADVAN subroutine (see Chapter 1, Section 3.2) which is called ADVAN2 (See Chapter 7). Figure 2.3 shows the part of the output of NONMEM for this problem that verifies the user’s choice of model. It also describes the features of the model in terms of its compartments. Of relevance to this problem are the DEPOT compartment (where the dose goes, and from which drug enters the central compartment by a first order process), and the CENTRAL compartment itself. Note, for example, that the default compartment for doses (i.e., where PREDPP will add doses if not otherwise instructed) is the DEPOT compartment, as it should be.
ONE COMPARTMENT MODEL WITH FIRST-ORDER ABSORPTION (ADVAN2)
MAXIMUM NO. OF BASIC PK PARAMETERS: 3
BASIC PK PARAMETERS (AFTER TRANSLATION):
ELIMINATION RATE (K) IS BASIC PK PARAMETER NO.: 1
ABSORPTION RATE (KA) IS BASIC PK PARAMETER NO.: 3
COMPARTMENT ATTRIBUTES
COMPT. NO. FUNCTION INITIAL ON/OFF DOSE DEFAULT DEFAULT
STATUS ALLOWED ALLOWED FOR DOSE FOR OBS.
1 DEPOT OFF YES YES YES NO
2 CENTRAL ON NO YES NO YES
3 OUTPUT OFF YES NO NO NO
Figure 2.3. The PREDPP output that verifies the user’s choice of model. Features of the model are discussed, such as the names and numbering of parameters, and the attributes of the various compartments in the model.
The fifth input record
(figure 2.1) signals the start of the user’s
specification of the model for the pharmacokinetic
parameters. This specification is given in the next 4 lines
of so-called abbreviated code (the $PK record, along
with this abbreviated code is called the $PK block). Some of
the parameters that NONMEM estimates are denoted by
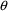 herein, and are labeled THETA in NONMEM input and output.
The model specified in figure 2.1 is very simple. It says
that a different unknown constant (NONMEM parameter) is to
be assigned to each pharmacokinetic parameter: first-order
absorption rate, KA (line 1 of the PK block, after the $PK
record - THETA(1)), rate constant of elimination, K (line 2
- THETA(2)), and volume of distribution, V (line 3 -
THETA(3)). The S2 parameter (a so-called scale parameter) is
discussed in Chapter 3, Section 2.2.
herein, and are labeled THETA in NONMEM input and output.
The model specified in figure 2.1 is very simple. It says
that a different unknown constant (NONMEM parameter) is to
be assigned to each pharmacokinetic parameter: first-order
absorption rate, KA (line 1 of the PK block, after the $PK
record - THETA(1)), rate constant of elimination, K (line 2
- THETA(2)), and volume of distribution, V (line 3 -
THETA(3)). The S2 parameter (a so-called scale parameter) is
discussed in Chapter 3, Section 2.2.
The sixth input record
(figure 2.1 -
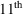 line) signals the start of the user’s specification of
the (statistical) model for the lack of fit of the
pharmacokinetic model to the data. This specification is
given in the next line of abbreviated code (the $ERROR
record, along with this line of abbreviated code is called
the $ERROR block). The model here says that observations
differ from predictions by an additive error
(ERR(1)).
line) signals the start of the user’s specification of
the (statistical) model for the lack of fit of the
pharmacokinetic model to the data. This specification is
given in the next line of abbreviated code (the $ERROR
record, along with this line of abbreviated code is called
the $ERROR block). The model here says that observations
differ from predictions by an additive error
(ERR(1)).
Record 7 ($THETA) gives
NONMEM information about possible values of each element of
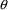 in the format: lower bound, initial estimate, upper bound.
When, as in this particular record, only two numbers are
given for an element of
in the format: lower bound, initial estimate, upper bound.
When, as in this particular record, only two numbers are
given for an element of
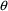 , these are understood to mean the lower bound and initial
estimate; the upper bound is unlimited. Record 8 ($OMEGA)
gives NONMEM an initial estimate of the variance of ERR(1).
This statistical parameter is often denoted by
, these are understood to mean the lower bound and initial
estimate; the upper bound is unlimited. Record 8 ($OMEGA)
gives NONMEM an initial estimate of the variance of ERR(1).
This statistical parameter is often denoted by
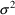 in statistical discussions, but with data from a single
individual, it is denoted by
in statistical discussions, but with data from a single
individual, it is denoted by
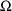 in NONMEM documentation, and by OMEGA in NONMEM input and
output. It is understood that a variance parameter is always
nonnegative. The $OMEGA record is further discussed in
Chapter 9, Section 3.
in NONMEM documentation, and by OMEGA in NONMEM input and
output. It is understood that a variance parameter is always
nonnegative. The $OMEGA record is further discussed in
Chapter 9, Section 3.
Record 9 ($ESTIMATION) instructs NONMEM to obtain estimates of the parameters, and the next record ($COVARIANCE) asks that it also obtain standard errors of the parameter estimates. The output is shown in figure 2.4. It requires little discussion. The first item, the minimum value of the objective function, is a goodness of fit statistic, much like a sum of squares (and as with a sum of squares, the lower the value, the better the fit). The parameter estimates (the parameter values at which the objective function is minimized) and their standard errors follow. Note that the estimate of OMEGA, too, has a standard error. Unlike most fitting programs, NONMEM treats this parameter like any other.
************************************************************************************************************************
******************** ********************
******************** MINIMUM VALUE OF OBJECTIVE FUNCTION ********************
******************** ********************
************************************************************************************************************************
************************************************** 8.940 **************************************************
************************************************************************************************************************
******************** ********************
******************** FINAL PARAMETER ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS *********************
TH 1 TH 2 TH 3
1.94E+00 1.02E-01 3.20E+01
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1
ETA1 8.99E-01
************************************************************************************************************************
******************** ********************
******************** STANDARD ERROR OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS *********************
TH 1 TH 2 TH 3
6.28E-01 7.35E-03 1.25E+00
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1
ETA1 5.44E-01
Figure 2.4. NONMEM output giving the goodness of fit statistic (the minimum value of the objective function) the parameter estimates, and their standard errors.
The next to last control record asks NONMEM to print a table displaying the input data and certain computed quantities. A portion of a NONMEM table is shown in figure 10.10 of Chapter 10. The last control record asks NONMEM to make a scatterplot of the prediction of each plasma concentration (PRED) VS the observed value (DV) and to draw the line of identity (UNIT, for "unit slope" line) on the plot. The plot is shown in figure 2.5.
PRED VS. DV
8.00E-01 2.34E+00 3.88E+00 PRED 5.42E+00 6.96E+00 8.50E+00
. . . . . .
. . . . . . . . . . .
7.00E-01. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.*. .
. . .
. . .
. . .
. . .
. . * .
. . .
. . .
. . .
2.26E+00. . ..
. . .
. . .
. . .
. . .
. * .
. . .
. . .
. . .
. . .
3.82E+00. . ..
. . .
. . .
. . .
. . .
DV . * . .
. . .
. . .
. . .
. . .
5.38E+00. * . ..
. . .
. . .
. . .
. . * .
. . .
. . .
. . .
. . .
. . * .
6.94E+00. . ..
. . .
. . .
. . .
. . .
. . .
. * . .
. . .
. . .
. * *.
8.50E+00. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
Figure 2.5. A scatterplot of the observed data (DV) vs the predictions of the best-fitting model parameters (PRED). The line of identity (intercept = 0; slope = 1) is drawn. If all points fell on that line, the fit would be perfect.
About 60 infants were
given phenobarbital therapeutically. A plasma concentration
was measured in each some hours after the first (loading)
dose, followed by multiple maintenance doses. A second, and
sometimes a third concentration were measured later. In all,
155 concentrations were observed. Figure 2.6 gives the
NM-TRAN control records. The data are too lengthy to show in
full, but figure 2.7 shows the data for the first
individual†.
----------
† File PHENO
of NONMEM distribution medium contains the complete data
set.
----------
Figures 2.8 - 2.10 have some relevant output. Again, most of the analysis results are apparent from the figures, and you should try to see if you can figure them out before going further. Note that the $INPUT record now defines a new data item, WT, the patient weight. It’s value is given on every data record for an individual, in the column indicated. This is so despite the fact that WT may not change within an individual. This is a bit repetitious, but convenient.
$PROBLEM PHENOBARB
$INPUT ID TIME AMT WT APGR DV
$DATA PHENO
$SUBROUTINE ADVAN1
$PK
TVCL=THETA(1)
CL=TVCL+ETA(1)
TVVD=THETA(2)
V=TVVD+ETA(2)
; THE FOLLOWING ARE REQUIRED BY PREDPP
K=CL/V
S1=V
$ERROR
Y=F+ERR(1)
$THETA (0,.0047) (0,.99)
$OMEGA .0000055, .04
$SIGMA 25
$ESTIMATION PRINT=5
$TABLE ID TIME AMT WT APGR
$COVARIANCE
$SCATTER PRED VS DV UNIT
$SCATTER RES VS WT
Figure 2.6. NM-TRAN control records for analysis of some population phenobarbital data.
1 0. 25.0 1.4 7 .
1 2.0 . 1.4 7 17.3
1 12.5 3.5 1.4 7 .
1 24.5 3.5 1.4 7 .
1 37.0 3.5 1.4 7 .
1 48.0 3.5 1.4 7 .
1 60.5 3.5 1.4 7 .
1 72.5 3.5 1.4 7 .
1 85.3 3.5 1.4 7 .
1 96.5 3.5 1.4 7 .
1 108.5 3.5 1.4 7 .
1 112.5 . 1.4 7 31.0
Figure 2.7. The first individual’s phenobarbital data.
The records are very similar to those for the theophylline problem. The new features are that the model has changed (it is implemented by ADVAN1, not ADVAN2), the model for the pharmacokinetic parameters is more complicated, and an additional scatterplot is requested. The data for each infant is similar to those shown in figure 2.7; however, now all of the data records for each infant start with the same value for the ID data item (column 1), but this value differs between infants.
ADVAN1 implements the one-compartment (monoexponential) model, without first order absorption. No absorption model was needed for this problem because all concentrations were measured many hours after the last (oral) dose, so absorption could be considered to be complete, and, for the purposes of data analysis, immediate.
The parameters of the one-compartment model are defined by the abbreviated code following the $PK statement: Clearance (CL) and Volume of Distribution (V). However, here each parameter is not simply equal to one of NONMEM’s parameters (an element of THETA). Rather, CL, for example, is equal to a parameter (THETA(1)) plus a new term, ETA(1). The latter expresses interindividual variability, and stands for the deviation of the individual’s true clearance (CL) from the population value (TVCL, Typical Value of CLearance, which, in turn, is simply THETA(1)). This model is essentially different from the theophylline model, because it incorporates interindividual variability (something that an individual model need not do). Note that since PREDPP ultimately needs the values of microconstants, rather than physiological-based pharmacokinetic parameters such as clearance, code must be given for K, the rate constant of elimination. There is, though, a simple alternative to writing this additional line of code. It is discussed in Chapter 3 Section 2.1.
The abbreviated code after the $ERROR record is exactly the same as that with the theophylline data and expresses the same model for lack-of fit between observations and predictions for an individual. The $OMEGA and $SIGMA records, which give NONMEM information about the estimated variances of the ETA and ERR variables, are discussed in Chapter 9, Section 3. Previously the initial estimate of the variance of ERR(1) was given on a $OMEGA record. Here it is given on a $SIGMA record. This difference in NONMEM conventions between individual type data and population type data will be discussed more fully in Chapters 3 and 4.
NONMEM is again instructed to estimate the parameters and their standard errors. The results are shown in figures 2.8 and 2.9.
************************************************************************************************************************
******************** ********************
******************** MINIMUM VALUE OF OBJECTIVE FUNCTION ********************
******************** ********************
************************************************************************************************************************
************************************************** 717.203 **************************************************
************************************************************************************************************************
******************** ********************
******************** FINAL PARAMETER ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS *********************
TH 1 TH 2
5.48E-03 1.40E+00
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1 ETA2
ETA1 6.85E-06
ETA2 0.00E+00 2.86E-01
SIGMA - COV MATRIX FOR RANDOM EFFECTS - EPSILONS ****
EPS1
EPS1 8.01E+00
Figure 2.8. NONMEM output giving the goodness of fit statistic (the minimum value of the objective function) and the parameter estimates for the phenobarbital problem.
************************************************************************************************************************
******************** ********************
******************** STANDARD ERROR OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS *********************
TH 1 TH 2
4.86E-04 7.84E-02
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1 ETA2
ETA1 2.27E-06
ETA2 ......... 8.34E-02
SIGMA - COV MATRIX FOR RANDOM EFFECTS - EPSILONS ****
EPS1
EPS1 1.49E+00
Figure 2.9. NONMEM output giving the standard errors of the parameter estimates for the phenobarbital problem.
Note that now there are estimates of the variances of the interindividual differences in CL (OMEGA - ETA1) and V (OMEGA - ETA2), as well as of the residual error variance (denoted by SIGMA in NONMEM output when the data are from a population; again, see Chapters 3 and 4). There are also standard errors for these estimates.
The next-to-last control record asks NONMEM to make the same kind of scatterplot as in the theophylline problem: a plot of the predictions vs the observations. Here, a prediction for an individual’s observation is based on typical (population) values of the pharmacokinetic parameters (see figure 2.8), rather than the values of the pharmacokinetic parameters for the specific individual. The plot is shown in figure 2.10.
PRED VS. DV
0.00E+00 2.60E+01 5.20E+01 PRED 7.80E+01 1.04E+02 1.30E+02
. . . . . .
. . . . . . . . . . .
5.00E+00. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . * .
. . .
. . .
. * .
. . .
. * * ** * * .
. * * ** * * * .
. .* .
. * *3 * * * .
1.80E+01. * *** *2 * ..
. * * 3*2 * .
. 2 * . *2 2* * * .
. *2 **2*. * * * * .
. *2* 2 . * * .
. *2 * ** * ** * .
. ** *** 3. * * * .
. * . 2 * * .
. * 2 . ** * * * .
. * * *.2 * * .
3.10E+01. * **** 2** ..
. * ** . .
. * 22* * * .
. * * . * .
. ** * . .
DV . * * ** * * * * .
. * * . .
. * * . .
. * . * .
. . .
4.40E+01. . ..
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
5.70E+01. . ..
. * . .
. . .
. . .
. . .
. . .
. . .
. . .
. * . .
. . .
7.00E+01. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
Figure 2.10. A scatterplot of the observed data (DV) vs the predictions with the best fitting model parameters (PRED). The line of identity (intercept = 0; slope = 1) is drawn. If all points fell on that line, the fit would be perfect. Here, in contrast to figure 2.5, the data arise from many different individuals. One cannot tell which data came from which infant.
Although the fit is fairly good, the points far to the right of the line of identity of figure 2.10 indicate that there are many predictions (PRED) that are much higher than their corresponding observations (DV). This is seen from another point of view in the second scatterplot. This scatterplot plots residuals (RES) vs patient weight (from the data item, WT — see figure 2.6). A residual is the difference between an observed concentration and its prediction (the same prediction used in the scatterplot of figure 2.10). The residuals reflect not only lack of fit between observations and predictions for a given individual (the variance SIGMA), but also interindividual variability (the variances comprising OMEGA). They can be thought of as reflecting the part of the data that the model does not explain. As can be seen from figure 2.11, there is a clear relationship between the sign and magnitude of the residuals and patient weight. Here, the patients with the largest weights have the most negative residuals; i.e., their predictions are much larger than their observations. These are the same points that fell on the far right of figure 2.10.
RES VS. WT
-9.00E+01 -6.60E+01 -4.20E+01 RES -1.80E+01 6.00E+00 3.00E+01
. . . . . .
. . . . . . . . . . .
5.00E-01. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . . .
. . .
. . * .
. *. *** 2 * **2 .
. . .
. . * 2 .
. * 23 2* * .
. . .
. * **. **23* .
. * 22 **2 4*3* * * .
1.14E+00. . ..
. * * .*2*42*** .
. *** 34** .
. . .
. * ***222224* .
. . .
. * ** ** ****** .
. . .
. . .
. * * ***3 * .
1.78E+00. **2 ** 2* ..
. . .
. ** * * .* .
. . .
. . .
WT . * * . .
. . .
. . .
. . .
. . .
2.42E+00. . ..
. 2 . .
. . .
. * . .
. . .
. . .
. * * . .
. . .
. . .
. . .
3.06E+00. . ..
. * * * . .
. 2 * * . .
. . .
. . .
. . .
. . .
. * * . .
. * * * . .
. . .
3.70E+00. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . . .
. . . . . . . . . . .
Figure 2.11. A scatterplot of the residuals (RES) vs patient weight (WT). The pattern suggests that observations are underpredicted in infants with low weight, and overpredicted in those with higher weights.
An obvious explanation is that Clearance or Volume, or both, increase with weight, so that without weight being taken into account, too high a prediction is being made for a larger infant and too low a prediction is being made for a smaller infant, all other things (i.e., dose) being equal. To see if accounting for weight improves the fit, the run specified in figure 2.12 can be done.
$PROBLEM PHENOBARB WITH WEIGHT IN MODELS FOR CL AND V
$INPUT ID TIME AMT WT APGR DV
$DATA PHENO
$SUBROUTINE ADVAN1
$PK
TVCL=THETA(1)+THETA(3)*WT
CL=TVCL+ETA(1)
TVVD=THETA(2)+THETA(4)*WT
V=TVVD+ETA(2)
; THE FOLLOWING ARE REQUIRED BY PREDPP
K=CL/V
S1=V
$ERROR
Y=F+ERR(1)
$THETA (0,.0027) (0,.70) .0018 .5
$OMEGA .000007, .3
$SIGMA 8
$ESTIMATION PRINT=5
$COVARIANCE
$TABLE ID TIME AMT WT APGR DV
$SCATTER PRED VS DV UNIT
$SCATTER RES VS WT
Figure 2.12. NM-TRAN control records for fitting a model taking into account the effect of patient weight to the population phenobarbital data.
Now both TVCL and TVVD are linear functions of weight with, in the case of TVCL, for example, intercept THETA(1), and slope THETA(3). Both slope and intercept are "population" parameters since they relate weight to typical population values of the pharmacokinetic parameter. Now we see why WT is given in every data record: the abbreviated PK code may need to be evaluated at each event time. If WT did not change over time within any patient, it could be given only on the first data record for each patient, but then slightly more complicated abbreviated code would be needed. The output from running the input of figure 2.12 is shown in figures 2.13 - 2.16.
************************************************************************************************************************
******************** ********************
******************** MINIMUM VALUE OF OBJECTIVE FUNCTION ********************
******************** ********************
************************************************************************************************************************
************************************************** 609.134 **************************************************
************************************************************************************************************************
******************** ********************
******************** FINAL PARAMETER ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS *********************
TH 1 TH 2 TH 3 TH 4
1.43E-11 1.21E-01 4.77E-03 9.18E-01
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1 ETA2
ETA1 1.36E-06
ETA2 0.00E+00 7.51E-02
SIGMA - COV MATRIX FOR RANDOM EFFECTS - EPSILONS ****
EPS1
EPS1 8.71E+00
Figure 2.13. The minimum objective function value and parameter estimates for the phenobarbital data, using the model of figure 2.12, which takes into account the effect of patient weight.
************************************************************************************************************************
******************** ********************
******************** STANDARD ERROR OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS *********************
TH 1 TH 2 TH 3 TH 4
9.49E-11 1.46E-01 2.24E-04 1.13E-01
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1 ETA2
ETA1 7.24E-07
ETA2 ......... 3.63E-02
SIGMA - COV MATRIX FOR RANDOM EFFECTS - EPSILONS ****
EPS1
EPS1 1.71E+00
Figure 2.14. The standard errors of the parameter estimates for the phenobarbital data, using the model of figure 2.12, which takes into account the effect of patient weight.
Note the improvement in the minimum objective function value (it drops 108 points), and the profound decreases in the sizes of the estimates of the interindividual variances; now that weight is in the model, there is less unexplained interindividual variability. As will be discussed in Chapter 5, the decrease in the objective function can be used for a formal hypothesis test of the appropriateness of the new model (figure 2.12) for the effect of weight on the pharmacokinetic parameters.
Note also the very small values estimated for THETA(1) and for its standard error. The intercept term of TVCL does not appear to be an important part of the model. This model is refined in Chapter 10, Section 6.2, where it is seen that deleting THETA(1) and THETA(3) produces a model that fits as well as the model including them.
PRED VS. DV
9.00E+00 1.78E+01 2.66E+01 PRED 3.54E+01 4.42E+01 5.30E+01
. . . . . .
. . . . . . . . . . .
5.00E+00. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. * .
. .
.. .
. * . .
. . .
. . * * ** ** .
. * * . * * ** * .
. * . .
. *** *2 * * .
1.80E+01. *.**3* * ..
. * 2*32 .
. *22* * * * * * .
. * *4** * . * 2 .
. *2 * * .* * * .
. * * 2* . * 2 * * .
. **2 2 * . ** * * .
. * 2 .* * .
. * ** 2 * . * * .
. * * * * * * * .
3.10E+01. * * 2* * * * * ..
. ** .* .
. ** ** * ** * . .
. * ** . .
. * * * . .
DV . * * * ** . * * * .
. * * . .
. ** . .
. * . * .
. . .
4.40E+01. . ..
. . .
. . .
. . .
. . .
. . .
. ..
. .
. .
. .
5.70E+01. ..
. * .
. .
. .
. .
. .
. .
. .
. * .
. .
7.00E+01. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
Figure 2.15. A scatterplot of predictions vs observations for the phenobarbital data, using the model of figure 2.12, which takes into account the effect of patient weight. Compare to figure 2.10.
The scatterplots (figures 2.15 and 2.16) confirm that the new model is an improvement: the group of points far to the right of the line of identity have disappeared from the PRED vs DV plot, and the plot of residuals vs weight no longer shows a pattern.
RES VS. WT
-1.70E+01 -1.00E+01 -3.00E+00 RES 4.00E+00 1.10E+01 1.80E+01
. . . . . .
. . . . . . . . . . .
5.00E-01. . . . . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . . . . . . . . . . . . . . . .
. . .
. * .
. * * * * * * * . 2* * .
. . .
. *** . .
. * * * *.* * * * * * .
. . .
. * * * * * ***** * .
. * * ** * *. * ** 22 *2 * 2 * .
1.14E+00. . ..
. * * * * * * **** * * * * * .
. * * ** * 3 . 2* * .
. . .
. * 2 ***2. ** * 2* * ** ** .
. . .
. * * 3 *. ** * * * .
. . .
. . .
. * *** . * * * * * .
1.78E+00. * * . 2* ** * * ..
. . .
. * * * ** .
. . .
. . .
WT . *. * .
. . .
. . .
. . .
. . .
2.42E+00. . ..
. . * * .
. . .
. . * .
. . .
. . .
. * * . .
. . .
. . .
. . .
3.06E+00. . ..
. * . * * .
. * * * * . .
. . .
. . .
. . .
. . .
. . 2 .
. * * * . .
. . .
3.70E+00. . . . . . . . . . . . . . . . . . . . . . . . ... . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
Figure 2.16. A scatterplot of residuals (RES) vs patient weight (WT) for the phenobarbital data, using the model of figure 2.12, which takes into account the effect of patient weight. Compare to figure 2.11.
The examples in this chapter illustrate some of the most important and useful features of NONMEM.
|
° |
NONMEM can fit both individual and population models. |
||
|
° |
NONMEM has a menu of pharmacokinetic models from which the one appropriate to the problem at hand can be chosen. |
||
|
° |
The user specifies the relationship of pharmacokinetic parameters to independent variables (such as WT in the phenobarbital example), using "population" parameters that will be estimated. |
||
|
° |
The user also specifies which parameters vary between individuals, and the form (model) for this variability, as well as the form (model) for the differences between observations from an individual and their predictions for this individual. |
||
|
° |
NONMEM estimates parameters describing both kinds of variability. |
||
|
° |
NONMEM provides estimates (standard errors) of the precision of its parameter estimates, including those describing variability. |
||
|
° |
NONMEM provides a means of deciding whether one model (e.g., that including weight’s effect on CL and V) fits the data better than another using the minimum objective function value, a goodness-of-fit statistic. |
||
|
° |
NONMEM provides (limited) graphics, useful in judging the adequacy of the model currently fit to the data. |