NONMEM Users Guide Part I - Users Basic Guide - Chapter A
A. Introduction and General Background
A.1. The NONMEM Program
A.2. Purpose and Organization of the Document
A.3. NONMEM Features
A.4. Major NONMEM Tasks
A.5. Random Interindividual Effects
A.6. Acknowledgements
NONMEM Users Guide Part I - Users Basic Guide - Chapter A
A. Introduction and General Background
A.1. The NONMEM Program
The NONMEM Project is an
undertaking by researchers in the Schools of Medicine and
Pharmacy of the University of California, San Francisco. The
project is a continually evolving one, aimed at providing
methodological results and computer tools for the analysis
of data that may be described by regression type models with
mixed effects, i.e. both fixed and random effects,
any of which may enter the model nonlinearly. Data of this
sort arise frequently in clinical pharmacological projects,
and to various degrees in other scientific fields. They
arise when there are multiple (or repeated) measurements
taken on a number of experimental units.
Version III Level 1 of NONMEM, a
computer program to analyze data using a nonlinear
mixed effects model, is now being
distributed. It is written in ANSI FORTRAN 77. It is
reliable, and attention has been paid to the input of
control information, to the output of results, and to
program diagnostics. The inputs to the program consist of
data files, control information, and user-coded subroutines.
The required formats for these inputs are not, however,
user-friendly. The NONMEM Project has paid more attention to
the development of more important aspects of the program -
that is until recently. At the same time as Version III is
being distributed the NONMEM Project is also distributing
for the first time another program, NM-TRAN, a preprocessor
to NONMEM that translates inputs specified in a more
user-friendly way to the formats required by NONMEM. This
translator is documented in NONMEM Users Guide IV, NM-TRAN
Guide. Also, much effort has been made to make NONMEM
efficient. However, this efficiency is measured with respect
to the types of computationally intensive tasks the program
performs, tasks that sometimes call for using a large-scale
computer, or a smaller dedicated machine.
Versions I-III incorporate an
important methodological restriction. Although fixed effects
may enter the model nonlinearly, random effects must enter
the model linearly. Therefore, the goal described at the
beginning of this section is not fully met. However, if a
model is contemplated in which some random effects enter
nonlinearly, it may often be approximated well-enough by a
model in which all random effects enter linearly. This
approximation is described in a number of references
(Sheiner et al 1977, Beal, 1984a), as well as being
illustrated in chapter F of this document. Research is in
progress within the NONMEM Project that could lead to a
future version of NONMEM in which this restriction is
relaxed. Except for the example discussed in chapter F, all
the examples in this document involve linearly occuring
random effects.
Another program restriction
concerns the number of possible levels of nesting of the
random effects. NONMEM provides only one level of nesting.
With one level of nesting there is one group of random
effects and another group nested within the first group.
This is usually adequate for pharmacokinetic and
pharmacodynamic applications. One advantage of NONMEM over
other programs for mixed effects models is that the random
effects in the first group can be multivariate, and the
random effects in the second group can be multivariate.
There really are two NONMEM
programs, single- and double-precision versions. The user
can choose to use either. Many problems with few parameters
to be estimated can be run successfully with the
single-precision version. Problems with many parameters
usually need double-precision arithmetic. If the
computational time requirement does not pose a particularly
difficult problem, the user should simply use the
double-precision version. This version is not simply the
single-precision version with all floating-point variables
and arrays declared double precision. Rather, care has been
taken to use double-precision only where it is necessary.
When the computational time requirement does pose a problem,
the user might first try using single-precision. If a
problem develops (see section C.3.5.1), then the user might
try using double-precision.
A.2. Purpose and Organization of the Document
This document, the Users Basic
Guide, is first of a six part series of user documentation
for the NONMEM system. The other five parts are:
Part II - Users Supplemental
Guide
Part III - NONMEM Installation Guide
Part IV - NM-TRAN Guide
Part V - NONMEM-PREDPP Introductory Guide
Part VI - PREDPP Guide
This first part contains the
essential information about how to use NONMEM. It is
presumed that the reader has had some previous experience
with using a nonlinear regresssion type program and that he
knows how to interpret the output from that program.
Part II contains supplemental
information about using NONMEM, and Part III contains
program installation information and describes the program
file structure. Part IV is a reference guide for NM-TRAN
(see section A.1). Part V is a primer designed for beginning
users who wish to use NONMEM for analyzing pharmacokinetic
data. For such users it might be helpful to begin by reading
Part V, rather than this document. Part VI contains detailed
user-information about PREDPP, a useful software package to
be used with NONMEM by those analyzing pharmacokinetic
data.
The Users Basic Guide is
organized around realistic examples, progressing from a
simple nonlinear regression example to an example of a
nonlinear model with several one-level nested random
effects. These examples are taken from the field of Clinical
Pharmacology. Thus those persons who are not very familiar
with nonlinear mixed effects models may, by carefully
following this progression of ideas, become more familiar
with the concepts. Presumably though, a NONMEM user is
familiar with simple nonlinear regression and has some
familiarity with mixed effects models; he understands that
he is faced with data manifesting several variance
components, and he knows how to begin to model his data in
terms of these components. As stated above, for the beginner
with pharmcokinetic data it might be helpful to first study
NONMEM Users Guide, Part V. With each example the inputs and
outputs of the program that pertain to that example and that
are not clear from the previous examples, are explained. The
experienced NONMEM user should be helped by the Appendix
which summarizes the program’s control records.
A.3. NONMEM Features
The important ability of NONMEM
to help analyze complicated statistical regression type
models has already been noted in section A.1. Other features
of the program are briefly listed here.
|
i |
|
Derivatives of the regression
function and certain weighting functions with respect to
model parameters need not be supplied. |
|
ii |
|
The estimates of fixed effect
parameters may be constrained. |
|
iii |
|
Initial estimates of the
parameters to be estimated need not be given. |
|
iv |
|
The iterative search involved in
obtaining the final parameter estimates has good convergence
behaviour even when parameter estimates are constrained
under a null hypothesis. |
|
v |
|
A file may be output at the end
of the search that allows the search to be conveniently and
smoothly continued (or computations depending on the results
of this search to be performed) in a subsequent run, without
once again starting the search from the beginning. |
|
vi |
|
An estimate of the covariance
matrix of the (parameter) estimate is carefully
computed. |
|
vii |
|
Tables and scatterplots of data
items, and also of predictions, residuals, and weighted
residuals, may be output. |
|
viii |
|
The amount of data that may be
input is not limited. |
|
ix |
|
Multiple problems may be
implemented during a single NONMEM run. |
Elaboration of some of these
features occurs in section A.4 below; all are treated in
detail in chapters C-F. Other less frequently used features
that are described in NONMEM Users Guide Part II are:
|
x |
|
Variance-covariance components
may also be constrained in certain ways. |
|
xi |
|
There is considerable
flexibility in defining the objective function. |
|
xii |
|
Transgeneration of the data may
occur before and after parameter estimates are obtained. |
|
xiii |
|
Data may be simulated (as well
as subsequently analyzed) under the specified model. |
|
xiv |
|
Eigenvalues of the estimated
correlation matrix of the (parameter) estimate may be
computed. |
One simple constraint on
covariance components, i.e. constraining all of these to be
zero, is described in Part I.
A.4. Major NONMEM Tasks
There are six major NONMEM tasks
that may be undertaken in any given NONMEM problem. These
six tasks are performed in what are called the six program
steps. Each of these steps are optional, though some step
depend on the results of previous steps.
In the first step, the
Simulation Step, data are simulated under the user-specified
model. The particulars of this step are discussed in NONMEM
Users Guide, Part II.
In the second step, the Initial
Estimation Step, initial estimates of model parameters are
computed. Initial estimates may be specified by the user,
and often this is not difficult. But on occasion some help
is needed, and the user may leave any particular initial
estimate blank, in which case the Initial Estimation Step is
executed.
In the third step, the
Estimation Step, final estimates of the model parameters -
fixed effect parameters and variance-covariance components -
are obtained. For this purpose an objective function (e.g. a
least squares objective function) in the model parameters is
minimized, and the final estimate (as a vector) is taken to
be the minimum point. The minimization is carried out by
implementing a numerical search in parameter space for the
minimum point. Actually, NONMEM reparametrizes the model,
the objective function is expressed internally in terms of
the new parameters, and the search is implemented in the
transformed parameter space. The default objective function
is the extended least squares objective function (Beal,
1984a,b) which is often appropriate with continuous-valued
type observations modeled in terms of a regression function
whose values predict these observations. There can be other
types of observations, e.g. dichotomous observations or
failure-time observations, where another objective function
would be more appropriate. NONMEM allows the user to define
many other types of objective functions.
The numerical search is
implemented according to an algorithm by R.A. Fletcher,
1972, modified by IMSL (whose code forms the basis for the
NONMEM code), and further modified by the NONMEM Project.
This algorithm is a derivative-free quasi-Newton type
minimzation algorithm for an arbitrary objective function.
It is presumed that the user has some familiarity with the
types of numerical problems that can be encountered with
minimization algorithms.
In the fourth step, the
Covariance Step, an estimate for the covariance matrix of
the estimate obtained in the Estimation Step is computed.
The accuracy of this covariance estimate increases as the
number of (statistically independent) observations
increases. It is not a simple matter to know how reliable
the covariance estimate is for any given problem. This
difficulty is encountered with any nonlinear regression
program. The examples used in this document involve only
moderate amounts of data, but in this respect they are
similar to many problems run over the years by NONMEM users.
On the other hand, the original impetus for the NONMEM
Project was to develop an ability to analyze large
quantities of pharmacokinetic data arising during routine
patient care, and the large data requirement underlying the
covariance estimate would not be a particular problem in
this context. In any case, some elements of the covariance
estimate may be better estimated than others. This goes
along with the fact that some model parameters may be better
estimated than others. For example, parameters in the
regression function are usually estimated better than
variance components, and variance components are usually
estimated better than covariance components. The covariance
estimate at least provides certain important qualitative
information. In this document it is called the covariance
matrix, for short, and the square roots of its diagonal
elements are the estimates of the standard errors of the
parameter estimates.
The covariance matrix involves
derivatives of the objective function with respect to model
parameters. These derivatives are computed numerically,
using a complex algorithm based in part on the method
described by Nelder and Mead (1964). In addition to
computations of the covariance matrix, computations of the
inverse covariance matrix, the standard error estimates, the
correlation matrix (derived from the covariance matrix), and
the eigenvalues of the correlation matrix are all performed
in the Covariance Step.
In the fifth step, the Tables
Step, all data items of selected types may be tabulated.
There can be several tables, and each table can be printed
or stored in a file. Each row of a table corresponds to a
different data record, and each column corresponds to a
different type of data item. With each data record there are
three additional types of data items, called the NONMEM
generated data items, which do not occur in the data set
itself, but they are included in all tables. As do the other
data items in the data record, these three data items relate
to the observation in the data record. With the default
objective function (i.e. the extended least squares
objective function) these three data items are: the
prediction of the observation, the residual difference
between observation and prediction, and the weighted
residual difference. With other user-defined objective
functions, other NONMEM generated data items can be defined.
Also, the rows of a table may be sorted on the data items of
one type, and then sorted within that sorting on the data
items of another type, etc.
In the sixth step, the
Scatterplot Step, data items of one type can be
scatterplotted against the data items of another type. A
scatterplot can be used to plot functions as well as
relationships that show "scatter". A scatterplot
of y vs x may also include the line y=x (useful when
prediction is scatterplotted against observation), and a
scatterplot of residual or weighted residual data items
always includes the "zero line". Moreover,
families of scatterplots of y vs x may be generated. Each
member of a family is obtained using only the data records
with the same value of some third data item type, u. A
family member exists for each different value of u occuring
in the data set. In addition, families, each of whose
members is obtained using only the data records with the
same values of some third and fourth data item types, u and
v, may also be generated. Using the transgeneration feature
(see NONMEM Users Guide, Part II), data items to be tabled
or scatterplotted may be defined in terms of the final
parameter estimate.
A.5. Random Interindividual Effects
Typically with population type
pharmacokinetic data, there are repeated observations, i.e.
measured responses, on each of a number of experimental
units. The experimental units are animal or human subjects,
and presumably, they are chosen randomly from the population
of interest. If there were no measurement error in the
responses, and if for fixed values for a set of measurable
independent variables, a subject always had the same
response, then usually, one would still not be able to
predict this response with full certainty. This is because
there are usually intersubject, or what we call
interindividual, differences in response which cannot be
explained solely in terms of the measureable independent
variables. Rather, they are attributable to effects whose
values are unknown and which we treat as random, and we call
these effects random interindividual effects. The
rationale for treating these effects as random is that as
individuals are randomly chosen, so are the interindividual
values associated with the effects in question. The values
of a random interindividual effect are constant for all
observations from a given individual. In the context of
NONMEM the values of a random interindividual effect, as
they vary from individual to individual, are to be regarded
as being statistically independent. The rationale for this
is that individuals are assumed to be chosen not only
randomly but also independently one from the other.
The values of random interindividual effects are unknown.
Fixed interindividual effects are the effects whose
values can be measured. (These need not be treated as
random, and so they are regarded as fixed.) The
concept of random interindividual effects is central to
NONMEM. This concept sets the program apart from other
nonlinear regression programs but makes it similar to other
repeated measures type programs.
With models where no random
effect is nested within another random effect, NONMEM treats
all random effects as random interindividual effects. In
other words, the values of all random effects vary only from
individual to individual. Consider, for example, any simple
nonlinear regression model. There is no nesting of random
effects since the model has only one random effect
(statistical residual effect). The value of this effect
varies from observation to observation, but each observation
can be identified with a different individual. Either each
observation indeed comes from a different individual, or
when the observations do not come from different
individuals, because these observations are regarded as
being statistically independent, then for the purposes of
modeling, they can be regarded as coming from different
individuals. (In the latter case, and when all observations
indeed come from a single individual, the population about
which inference is made is, of course, this individual.)
Therefore, the random effect can be (and with NONMEM it is)
treated as a random interindividual effect.
With models where there is a
one-level nesting of random effects NONMEM treats the random
effects in the group at the outside of the nest as random
interindividual effects. NONMEM treats the random effects in
the nested group as random intraindividual effects.
Their values vary from observation to observation within an
individual. In this context by an observation we mean either
a univariate observation, or, when appropriate, a
multivariate observation.
The random interindividual
effects are denoted by
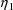 ,
,
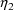 , etc. Their variance-covariance matrix is denoted by
, etc. Their variance-covariance matrix is denoted by
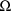 and is called OMEGA in the NONMEM printout. The random
intraindividual effects are denoted by
and is called OMEGA in the NONMEM printout. The random
intraindividual effects are denoted by
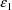 ,
,
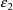 , etc. Their variance-covariance matrix is denoted by
, etc. Their variance-covariance matrix is denoted by
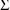 and is called SIGMA in the NONMEM printout.
and is called SIGMA in the NONMEM printout.
A.6. Acknowledgements
Many scientists have worked
closely with the NONMEM Project Group, and by using NONMEM
and providing helpful feedback, have greatly contributed to
its development. Many NONMEM users have on occasion also
shared their experience. We hope that the user-community
will continue to feel free to report successes and failures
so that the program can be further evaluated and modified in
ways from which everyone can benefit.
IMSL has also greatly
contributed to NONMEM development by entering into an
agreement with the NONMEM Project wherein some IMSL
proprietary software can be incorporated into the NONMEM
system.
The examples used in this
document involve theophylline data that was kindly
contributed for this purpose by Drs. Sidney Riegelman and
Robert Upton.
Financial support for the
development of NONMEM has come from NIH grants GM-16496 and
GM-26676 and from license fees paid by NONMEM users to the
University of California. Computing assistance has been
obtained from The Health Sciences Computing Facility, UCLA,
supported by NIH Special Research Resources grant RR-3.
TOP
TABLE OF CONTENTS
NEXT
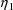 ,
,
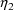 , etc. Their variance-covariance matrix is denoted by
, etc. Their variance-covariance matrix is denoted by
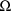 and is called OMEGA in the NONMEM printout. The random
intraindividual effects are denoted by
and is called OMEGA in the NONMEM printout. The random
intraindividual effects are denoted by
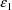 ,
,
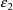 , etc. Their variance-covariance matrix is denoted by
, etc. Their variance-covariance matrix is denoted by
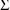 and is called SIGMA in the NONMEM printout.
and is called SIGMA in the NONMEM printout.